![]()
Gradient of a line
The gradient of a line is defined to be the gradient of any interval within the line.
This definition depends on the fact that two intervals on a line have the same gradient.
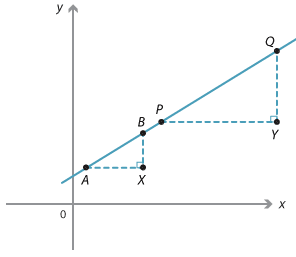
Suppose AB and PQ are two intervals on the same straight line.
Draw right-angled triangles ABX and PQY with sides AX and PY parallel to the x-axis and sides BX and QY parallel to the y-axis.
Triangle ABX is similar to triangle PQY since the corresponding angles are equal. Therefore:
\(\dfrac{QY}{PY}=\dfrac{BX}{AX}\).
That is, the intervals have the same gradient.
Example 4
Find the gradient of the line passing through the points:
- A(1, 4) and B(5, 12)
- C(6, –5) and D(–4, 2)
Solution
- The gradient of the interval \(AB =\dfrac{y_2 − y_1}{x_2 − x_1} =\dfrac{12 − 4}{5 −1} = \dfrac{8}{4} = 2\)
Therefore the gradient of the line AB = 2. - The gradient of the interval \(CD =\dfrac{y_2 − y_1}{x_2 − x_1} =\dfrac{2 −(−5)}{−4 − 6} = \dfrac{7}{−10}\)
Therefore the gradient of the line \(CD = −\dfrac{7}{10}\).